
Парадоксальные свойства пограничных пленок
Несколько неожиданных открытий пролило новый свет на физическую структуру микрослоев воды и воздуха, лежащих на границе океан - атмосфера. Оказалось, что несмотря на подвижность и податливость этой границы возмущающим воздействиям, несмотря на течения и волны, структура пограничных микрослоев принципиально не отличается от того, что возникает в жидкости или газе на границе с твердым телом.
Представим, что спокойный ламинарный поток, т. е. плавное упорядоченное движение, в котором струйки окрашенной жидкости параллельны друг другу, вступает в соприкосновение с твердой пластинкой или стенкой, расположенной параллельно потоку. Лабораторные опыты показывают, что ламинарное движение вблизи стенки при определенных условиях, зависящих от скорости потока - и шероховатости стенки; разрушается. Возникает зона, где окрашенные частицы приобретают беспорядочное вихревое движение. Эту зону называют турбулентным пограничным слоем.
Микроскопические наблюдения за прилегающей к стенке жидкостью открывают парадоксальное явление. С одной стороны, именно стенка, и ничто иное, вызывает турбулентные возмущения в потоке и создает перемешанный пограничный слой. С другой стороны, та же стенка гасит турбулентные пульсации и уничтожает турбулентный режим в непосредственной близости.
Непримиримое, казалось бы, противоречие имеет объяснение. Стенка останавливает и как бы прикрепляет к себе ближайшие частицы жидкости. Между жидкостью, прилипшей к стенке (так называемый слой прилипания), и потоком возникает градиент скорости. Этот градиент и есть источник беспорядочных пульсаций турбулентной природы и перехода механических движений в тепло.
Обозначим скорость генерации турбулентных движений
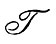
a тепловых
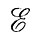
и сравним характер этих процессов:
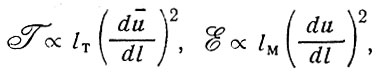
где α - знак пропорциональности, l - расстояние от стенки, lм - длина свободного пробега молекулы, lт - длина переноса при турбулентной пульсации.
Таким образом, существует положительная обратная связь: чем меньше проявление турбулентности lт, тем меньше ее генерация
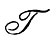
В 1950 г. немецкий гидродинамик Г. Шлихтинг [1956] писал: «В очень тонком слое в самой непосредственной близости от стенки всякое турбулентное течение ведет себя в основном как ламинарное течение. В таком тонком слое, называемом ламинарным подслоем, ... не может существовать турбулентность». И далее: «Толщина ламинарного подслоя обычно столь мала, что практически она либо совсем не может быть измерена, либо может быть измерена только с очень большим трудом».
Шлихтинг рисует трехслойную структуру течения на границе с твердым телом: «ламинарный пограничный подслой», «переходная область», «собственно турбулентный пограничный слой».
Все было бы хорошо, но непонятно, чем ламинарный подслой экранирован от проникновения турбулентных пульсаций извне- Советские гидродинамики А. С. Монин и А. М. Яглом [1965], ссылаясь на ультрамикроскопические наблюдения 1932 г. за движением частиц, взвешенных в жидкости около стенки, и на более поздние наблюдения, утверждают, что движение в пограничном подслое, несмотря на ламинарный профиль скорости, сопровождается заметными турбулентными пульсациями, и поэтому термин «ламинарный подслой» считают мало удачным. Монин и Яглом предлагают заменить его термином «вязкий подслой». Так как динамику подслоя определяет молекулярная вязкость, то существует еще и третье название его - «молекулярный подслой» (известно понятие «турбулентная вязкость», которое можно распространить на весь пограничный слой). Тепло и растворенные вещества передаются через подслой преимущественно процессами молекулярной теплопроводности и молекулярной диффузии. Поскольку молекулярная передача осуществляется очень медленно, то в молекулярном подслое возникают огромные градиенты свойств, устанавливается особая температура и состав воды.
Очевидно, что условия на подвижной, пульсирующей границе вода - воздух значительно отличаются от условий на твердой стенке. Поэтому открытие в этих условиях вязкого подслоя было связано с исключительными техническими трудностями и оказалось для большинства океанологов ошеломляющей неожиданностью. И вот доказано существование молекулярного подслоя и в воде, и в атмосфере, прилегающей к границе раздела вода-воздух, доказано прямыми измерениями в реках, озерах, море и океане.
Летом 1973 г. на Балтийском море у прибрежного города Цингст ученые ГДР и СССР П. Хупфер, Т. Фокен и Г. Панин [Hupher e.a., 1975] провели тонкие наблюдения молекулярного воздушного подслоя. Существование подслоя определялось с помощью самописца температуры системы «падающий зонд» (фаллзонд) с разрешающей способностью по температуре 0,02°С и по высоте 0,02 мм. Согласно теории теплопроводности, в пределах молекулярного подслоя температура с высотой должна в установившемся состоянии изменяться линейно, что соответствует постоянному значению коэффициента молекулярной теплопроводности. Подкрепим это важное положение простым доказательством. Молекулярный поток тепла g, пересекающий за единицу времени площадку
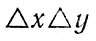
равен, согласно экспериментально установленному физическому закону,
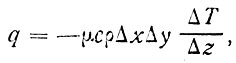
(48)
где μ - коэффициент температуропроводности, с -теплоемкость, р - плотность воды, Т - температура, z - вертикальное расстояние.
Когда поток тепла постоянен, распределение температуры не изменяется во времени. Но если в каком-то элементарном объеме пространства
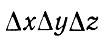
величина входящего потока больше, чем выходящего, температура в точке, окруженной этим объемом, должна повышаться. Скорость изменения температуры можно найти, записав разность величин входящего и выходящего потоков тепла. При постоянном значении μ запись будет иметь вид
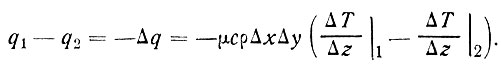
(49)
Разделим балансовое уравнение (49) на массу объема
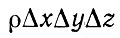
и теплоемкость. Тем самым мы отнесем величину накопления тепла к единице массы и переведем теплоту в температуру. Заменив одновременно с этим конечные разности бесконечно малыми, получим балансовое уравнение скорости изменения температуры в точке

(50)
где t - время.
Условие стационарного распределения температуры (dТ/dТ = 0) выражается требованием
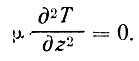
(51)
Очевидно, что равенство (51) соответствует утверждению: распределение температуры имеет вид прямой линии, ибо только для прямой вторая производная равна нулю.
Если бы величина коэффициента температуропроводности μ изменялась по оси z, мы не имели бы права вынести μ за скобки в формуле (49), а вместо равенства (51) получили бы условие
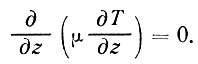
(52)
Это выражение нам понадобится позже для вывода не линейного, а логарифмического характера изменения поля загрязнений вблизи берега. Теперь же вернемся к наблюдениям вблизи Цингста. Молекулярный пограничный подслой регистрировался неизменно при скорости ветра до 7 м/с и направлении его с моря и с суши. Толщина подслоя менялась от 10 мм и более при мало-ветрии до долей миллиметра при усилении ветра и в среднем была несколько менее 1 мм. Зависимость толщины подслоя от скорости ветра была выражена наблюдателями следующей приблизительной эмпирической зависимостью:
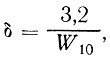
(53)
где W10 - скорость ветра на высоте 10 м над уровнем моря, в м/с; δ - толщина подслоя, в мм.
Перепад температуры между верхней и нижней границами слоя достигал в отдельных случаях 10С, что соответствовало громадному температурному градиенту 1000°С/м. Пример такой записи показан на рис. 17.
Одно из удивительных свойств молекулярного воздушного подслоя состоит в том, что он часто, оказываясь легче вышележащего воздуха, вносит резкую неустойчивость в стратификацию приводного слоя.
Существование подслоя молекулярной теплопроводности на поверхности воды зарегистрировали значительно раньше, чем в воздухе. В 1934 г. советские ученые В. К. Альтберг и Е. А. Попов, измеряя с помощью миниатюрных термосопротивлений температуру в поверхностном слое реки Невы, на горизонтах, разделенных 2-миллиметровыми интервалами, получили, что на поверхности воды почти на 0,5°С холоднее, чем на глубине 2 мм.

Рис. 17. Запись температуры в ламинарном пограничном слое воздуха над Балтийским морем у побережья при скорости ветра 3,6 м/с, δ - толщина слоя. dТ/dz - градиент температуры в слое, Q - поток тепла через слой.
Такой перепад соответствует температурному градиенту 250°С/м. В 1960 г. американские ученые Г. Ивинч и Е. Мак-Алистер у побережья Калифорнии с помощью радиационного термометра наблюдали исчезновение холодной пленки в момент разрушения волн. Пленка восстанавливалась примерно через 12 секунд после разрушения. Обширные наблюдения (около тысячи) провел с использованием радиометра и термометра сопротивления С. П. Малевский-Малевич в Атлантическом океане и на Валдайском озере (1965-1969 гг.). Молекулярную пленку регистрировал при волнении и ветре до 10 м/с. В 83% наблюдений пленка имела отрицательную аномалию температуры, в 8% - по. ложительную. Отрицательные отклонения обычно составляли около 0,5°С, иногда превышали 1°С. Данные наблюдений в океане и озере оказались очень похожими [Малевский-Малевич, 1974]. Непрерывные записи температуры внутри пленки осуществили в 1971 - 1975 гг. на Черном море ученые физического факультета МГУ. Их термозонд регистрировал изменения температуры с точностью 0,05°С, инерционность прибора имела порядок 10-3 с. Зонд рассекал слой - 30 см воздуха и 30 см воды-со скоростью 17 см/с. 60-сантиметровый профиль записывался в одном масштабе, а температура в прилегающем к воздуху слое воды толщиной 8 мм - в масштабе, в 70 раз большем. На рис. 18, взятом из публикации Е. Г. Андреева, В. В. Гурова, Г. Г. Хунджуа [1976], левая кривая представляет собой растянутый в 70 раз отрезок а-в, который выглядит на правой кривой почти горизонтальным участком и соответствует поверхностному слою большого градиента температуры. Авторы пишут: «Впервые прямым методом показано, что на поверхности моря существует тонкий инверсионный слой толщиной 0,2-0,6 мм, коэффициенты обмена в котором равны значению молекулярного коэффициента теплопроводности воды при температуре 20°С».
![Рис. 18. Запись температуры в слое воздух - вода толщиной 60 см; слева - в увеличенном масштабе температура в холодной пленке воды толщиной 8 мм, Черное море [Е. Г. Андреев и др., 1976].](pic/000120.jpg)
Рис. 18. Запись температуры в слое воздух - вода толщиной 60 см; слева - в увеличенном масштабе температура в холодной пленке воды толщиной 8 мм, Черное море [Е. Г. Андреев и др., 1976].
На большем удалении от поверхности профиль начинает искривляться, и это свидетельствует о возрастании коэффициента теплопроводности с появлением элементов турбулентного перемешивания. Кривая имеет логарифмический характер, а это, как мы увидим дальше, означает линейное увеличение теплопроводности с глубиной.
|
ПОИСК:
|
© UNDERWATER.SU, 2001-2019
При использовании материалов проекта активная ссылка обязательна:
http://underwater.su/ 'Человек и подводный мир'
При использовании материалов проекта активная ссылка обязательна:
http://underwater.su/ 'Человек и подводный мир'