Поверхностное сгущение свойств

Пограничные эффекты давно уже породили и вопрос об общих путях математического описания термодинамических свойств систем, содержащих поверхности раздела. Для этого Дж. В. Гиббс ввел понятие поверхностное сгущение свойств.

Игнорируя границы раздела фаз, мы обычно задаем концентрацию какой-либо компоненты как число ее молей, производя суммирование по всем объемам различных фаз,

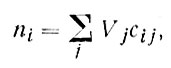
(1)

где j - индекс фазы, содержащей i-ю компоненту; Vj - объем каждой из фаз; сij - молярная концентрация i-й компоненты в j-й фазе.

Точно так же свободная энергия всей системы F рассчитывается суммированием по объемам фаз удельных (приходящихся на единицу объема) свободных энергий отдельных j-x фаз

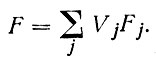
(2)

Согласно Гиббсу, для учета пограничных эффектов необходимо вести суммирование не только по объемам фаз, но и по всем площадям различных поверхностей их разделов s_k:

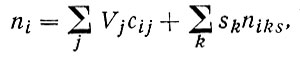
(1')

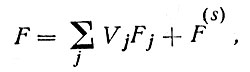
(2')

где s_kn_iks и F^(s) - соответственно поверхностные сгущения i-й компоненты на k-й границе раздела и свободной энергии.

Точно так же можно рассматривать поверхностное сгущение любого другого свойства системы: энтропии S^(s) , полной энергии U^(s), теплоемкости и т. д. Именно эти сгущения свойств, избытки энергии, энтропии, числа молей компонент - характеризуют отличие поверхностного слоя от объемных фаз. Поэтому удобно говорить не о всей энергии или энтропии поверхностного слоя, описываемых уравнениями вида (1') и (2'), а только о вторых слагаемых в этих уравнениях, описывающих избыток свойств (энергии, энтропии и т. д.) в объеме поверхностного слоя над их значениями в объеме внутри фаз. Для краткости эти избыточные свойства обозначают как поверхностные (например, свободная поверхностная энергия), помечая их верхним индексом s,

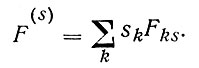
(3)

Однако, поскольку эти поверхностные термодинамические функции F^(s) , S^(s) , U^(s) и т. д. зависят от площади поверхности раздела s (индекс k далее для простоты опустим, т. е. будем говорить лишь об одной поверхности раздела), оказывается невозможным сравнивать между собой разные системы. Поэтому прибегают к удельным величинам, отнесенным к единице поверхности раздела s, отмечая их нижним индексом s в случае термодинамических функций и специальной буквой - для сгущения концентрации:

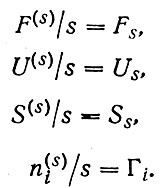
(4)

Введенная Гиббсом величина Г_i представляет собой, таким образом, удельное поверхностное сгущение концентрации- приходящихся на единицу площади поверхностного слоя избыток числа молей компоненты i в объеме поверхностного слоя над числом молей в таком же объеме внутри фазы. Эту величину называют абсолютной величиной гиббсовской адсорбции или просто адсорбцией компоненты i на данной поверхности.

Свободная поверхностная энергия F^(s) при постоянных температуре и составе поверхностного слоя равна работе A^(s) которую необходимо затратить на образование новой поверхности: F^(s)=A^(s) или, если все относить к единице новой поверхности,

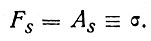
(5)

Эту работу образования единицы новой поверхности называют межфазным поверхностным натяжением и обозначают буквой σ оно аналогично давлению в объемной фазе. Величину σ можно рассматривать как удельную свободную поверхностную энергию F_s и как силу, действующую на единицу длины контура поверхности раздела фаз. Значения σ обычно приводятся для границы с вакуумом, они равны: для воды 73, поваренной соли 150, кварца 980, для алмаза 11400 эрг/см².

Полную поверхностную энергию можно определить из общего уравнения для внутренней энергии системы

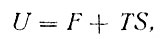
(6)

где TS - тепловой эффект процесса, энтропия S = - dF/dT.

Применительно к образованию единицы новой поверхности из уравнения (6), учитывая (5), получим уравнение Гиббса - Гельмгольца

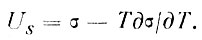
(7)

Так как поверхностное натяжение всегда уменьшается с ростом температуры (дσ/дТ<0), удельная поверхностная энергия всегда больше поверхностного натяжения. Так, для воды при 0>^°С (273 К) дσ/дТ ≈ -0,152 эрг/(см²-К) и U_s больше, чем σ, на величину 273x0,152 = 46 эрг/см², т. е. более чем в полтора раза.

В многокомпонентной системе полная удельная поверхностная энергия изменяется линейно с изменением адсорбции компонент

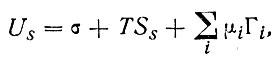
(8)

где коэффициент пропорциональности μ_i - химический потенциал i-й компоненты; химический потенциал является частной производной термодинамических потенциалов по массе i-й компоненты при постоянстве определенных условий, в том числе масс остальных компонент (обозначается индексом

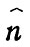
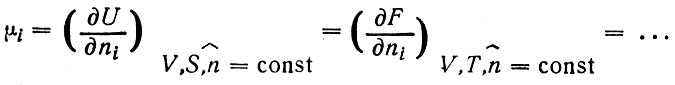
Из уравнения (8) для постоянной температуры и условий равновесия можно получить так называемое адсорбционное уравнение Гиббса

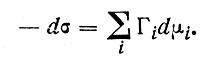
(9)

Опуская для упрощения нижние индексы (что соответствует одному адсорбирующемуся веществу) и учитывая, что d_μ = RTdlnyc, где R - газовая постоянная, получим адсорбционное уравнение Гиббса, в которое входит изменение поверхностного натяжения с изменением концентрации (дσ/дс),

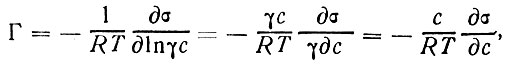
(10)

где коэффициент пропорциональности у- так называемый коэффициент активности данной компоненты.

Вещества, понижающие поверхностное натяжение, называются поверхностно-активными веществами, или коротко ПАВ, для них дσ/дс<0 и Г>0 (положительная адсорбция). Предельное значение понижения поверхностного натяжения с возрастанием концентрации, т. е. величина - (дσ/дс)_c→∞, называется поверхностной активностью. Из уравнения (10) следует, что могут существовать вещества с отрицательной адсорбцией (Г<0), если они повышают поверхностное натяжение (дσ/дс>0), т. е. поверхностно-инактивные вещества (ПИВ). Действительно, и ПАВ, и ПИВ есть, и они существуют в морской воде, влияя на формирование самых верхних пограничных слоев в океане.