Модели и оригинал

Современные экспериментальные средства позволяют проводить очень тонкие измерения температуры и концентрации в пограничных слоях и их изменений с удалением от поверхности раздела. Однако измерения скорости превращения веществ непосредственно в океане оказываются, как правило, невозможными.

Зная картину распределения концентрации субстанции (поле концентрации), можно оценить не только скорость ее превращения и перемещения, но и соответствующую удельную скорость, что гораздо важнее, так как это позволяет рассчитывать и прогнозировать такие состояния системы, которые отличаются от наблюдавшихся, например, гораздо большей концентрацией субстанции. Но для этого надо знать уравнение динамики процесса. Тогда, решая обратную задачу, по полю концентрации можно получить многие из интересующих величин.

Например, если в море, в котором можно пренебречь горизонтальными градиентами, измерено распределение радиоактивного изотопа, используются уравнения турбулентной диффузии этого радиоизотопа и солей:

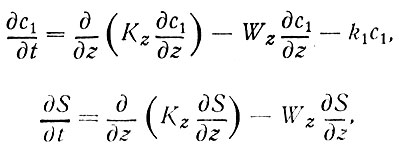
(11)

где c₁ - концентрация радиоизотопа, k₁ - постоянная его распада, K_z - коэффициент вертикальной турбулентной диффузии, W_z - вертикальная составляющая скорости течения, S - соленость.

Зная постоянную распада k₁ и используя графики распределения c₁ и S, можно решить обратную задачу (11) - определить параметры К_z и W_z. Ошибка здесь связана с неустойчивостью решения обратной задачи (11) - сильным возрастанием ошибки расчета при небольшом увеличении ошибки наблюдения, в этом в основном повинны вторые производные. Избежать сильного влияния вторых производных на ошибку расчета можно, избавившись от них, т. е. используя интегральные алгоритмы [Беляев, 1973, 1973а, 1978].

Если одновременно известно поле концентрации вещества, подвергающегося превращению, например загрязнения с2, то, используя уже известные значения К_z и W_z и уравнение турбулентной диффузии для этого вещества можно также решить обратную задачу и получить значение удельной скорости его превращения (константу скорости) k₂.

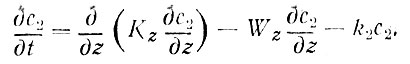
(12)

Однако, если вещество вообще не распадается, k₂ = 0, если существует его источник вне границы раздела (внутри вод) или если оно распадается совершенно по другому закону, все равно будет получено некоторое значение k₂, которое сколь угодно сильно может отличаться от действительной удельной скорости превращения вещества.

Неединственность решения обратных задач сильно ограничивает возможности использования полей концентрации для расчетов и интерпретации. Поэтому большие надежды возлагаются на реальные (лабораторные) модели, имитирующие условия, которые наблюдаются в природе, - имитирующие оригинал. Но при этом возникают свои, часто непреодолимые трудности.

Если мы точно сохраним все геометрические пропорции в реальной модели по сравнению с оригиналом (данным морем, океаном), т. е. добьемся геометрического подобия, то этим мы никак не обеспечим подобия гидродинамических режимов и полей концентрации. Если же добьемся подобия полей концентрации в модели и оригинале, то нарушим геометрическое и гидродинамическое подобие.

Этот порочный круг легко увидеть даже на примере оседания взвешенного вещества, консервативного, т. е. не претерпевающего превращения (трансформации).

Гидродинамический критерий подобия Рейнольдса

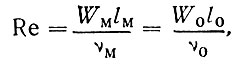
(13)

где нижними индексами «м» и «о» отмечены соответственно модель и оригинал, W - скорость потока, l - линейный размер, v - вязкость, требует увеличения скорости потока при уменьшении размера модели, чтобы не исказить в модели гидродинамический режим.

Однако, чтобы сохранить одинаковые условия оседания частицы в модели и оригинале, необходимо совпадение в них и значения критерия Фруда.

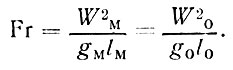
(14)

Но критерий Фруда, наоборот, требует уменьшения скорости потока в тех же условиях. Чтобы совместить критерии Re и Fr, не изменяя гравитационного ускорения g и сохраняя геометрическое подобие, мы должны использовать не воду, а другую жидкость, необходимую вязкость которой можно рассчитать по соотношению, получающемуся из сопоставления (13) и (14),

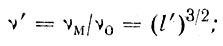
здесь штрихом отмечено соотношение величин в модели и оригинале.

Однако и при этом нам надо еще добиться подобия других явлений, с которыми связано оседание взвешенных частиц: флокуляции, коагуляции, плотностных потоков. Для подобия последних необходимо, чтобы выполнялось соотношение

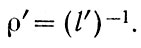
Следовательно, при уменьшении размера модели по сравнению с оригиналом надо во столько же раз увеличивать масштаб плотност-ного потока - концентрацию частиц.

Если же учесть, что взвесь разлагается, как это происходит с детритом в океане, то трудности неимоверно возрастут. Для трансформирующегося вещества необходимо выполнение еще и химического критерия подобия Дамкеллера

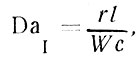
который опять-таки, как легко увидеть из сравнения выражений (15) и (13), несовместим с критерием Рей-нольдса. Чтобы добиться их совмещения, надо подбирать скорость трансформации вещества r, не меняя значений концентрации вещества с, что возможно лишь, если вместо данного изучаемого вещества использовать совсем другое.

Получается, что чем точнее в реальной модели мы копируем природу, тем дальше уходим от правильного ответа. Это происходит из-за того, что нам только кажется, будто мы все в модели изменяем в одной и той же пропорции, в действительности же мы не меняем силу тяжести, коэффициент молекулярной диффузии, механизм перехода ламинарного течения в турбулентное и многое другое. Поэтому, чтобы изучить процессы в море с помощью лабораторной модели, мы вынуждены пользоваться не водой, а маловязким раствором ПАВ, не ядохимикатом, который изучаем, а сахаром. Однако все эти усилия напрасны, так как мы не коснулись еще экологических критериев подобия, - ведь в океане трансформация веществ, в том числе загрязнений, идет в основном микробиологическим путем. Экологические же критерии подобия не установлены, и вопрос о них, по-видимому, никто никогда не ставил [Айзатуллин, Лебедев, 1977].

Поскольку в экосистеме процессы, и гидромеханические, и физические, и химические, и биологические, одновременны, видимо, обнаружится, что экосистемы не имеют себе подобных; следовательно, в лабораториях моделирование экосистем и трансформации веществ в них неосуществимо и пока во всяком случае является самообманом.

Выход из этой неприятной ситуации лежит через математическое моделирование, которое должно сочетаться с лабораторным экспериментом для установления параметров математических моделей, не зависящих от концентрации веществ, условий перемешивания, концентрации и активности организмов, а также через сочетание их с натурными наблюдениями.

Математическое моделирование тоже сталкивается с многочисленными трудностями, но они не носят такого принципиального характера и вполне преодолимы, правда при большой затрате сил и определенной организации исследований. Сложности здесь возникают из-за большого числа взаимосвязанных процессов, которые обычно исследуются в рамках разных научных дисциплин.

Принято выделять два подхода к преодолению трудности: классический физический подход и системный.

Классический физический подход, по замечанию Макса Борна, принес физикам дурную славу, но, без сомнения, позволил добиться выдающихся успехов. Он заключается в выделении одного, но фундаментального аспекта поведения системы; в массе частностей выявить ее большой лик (если пользоваться выражением Л. А. Зенкевича) позволяют генерализованные математические модели, которым отдается предпочтение при классическом подходе.

С системным подходом, в частности с системным анализом - методологией всеаспектного систематического рассмотрения крупных комплексных проблем, наоборот, принято связывать детальное, «на грани нашего понимания», описание системы и всех процессов с помощью ЭВМ, их имитацию на ЭВМ. Но это недоразумение. Хотя при системном анализе [Квейд, 1969] должны учитываться все факторы, какие могут сказаться на решении проблемы, при построении математической модели учитывают лишь важнейшие из них, т. е. задача также упрощается. Переусложнение модели (overfitting) признается опасной тенденцией, а всеохватность и универсальность ее (если под этим понимать способность ответить на любой вопрос) - недостижимыми. Стремление строить такие модели считается ошибочным. В этой связи экологи говорят о карикатурных моделях, ориентированных на передачу лишь самых существенных черт оригинала, и о портретных (фотографических) моделях, с помощью которых стремятся передать (имитировать) все детали облика оригинала.

В системном анализе предпочтение отдается первым, и модели используются как важное, но лишь вспомогательное, техническое, средство организации мышления и исследования [Квейд, 1969]. Считается, что результат системного анализа не может быть ошибочным, поскольку при его проведении учитываются все сколько-нибудь существенные аспекты. Отсюда следует: раз результат ошибочен, анализ не был системным, даже если использовались самые сложные модели.

С генерализованными, упрощенными, моделями, но не математическими, а графическими, имеют дело и в географии. Эти модели - географические карты. Упрощение, отражение в них лишь одного, самого важного в данном случае, аспекта (физико-географического, биогеографического); генерализация их (устранение излишне подробных деталей) позволили уже давно увидеть большой лик поверхности планеты, и он отражается картами более глубоко, чем непосредственными спутниковыми фотографиями.