Идеальный океан

Итак, наша цель - обсудить обобщенную (генерализованную) и предельно простую модель структуры океана в целом. Эта модель будет, с одной стороны, географической, поскольку она претендует на отражение обобщенной географической действительности и направляет внимание на совокупность физических, химических и биологических свойств, а с другой - моделью полностью абстрагированной от пространственных очертаний океана. Важнейшими элементами модели окажутся граничные поверхности океана, через которые осуществляется его обмен и взаимодействие с атмосферой, литосферой, живым веществом и космосом.

Начнем с необычного и абстрактного вопроса: «Можно ли создать словесное изображение или дать математическое описание еще не исследованного или даже не открытого океана (расположенного, допустим, вне Земли)?» Оказывается, что в этом направлении удается сделать определенные шаги при условии, что структура океана формируется под действием универсальных физических, химических и биологических законов. Сколь бы скромными ни были на этом пути результаты, они интересны тем, что связаны с необходимостью различить в океанической природе закономерности обязательные и повсеместные - наиболее общие, с одной стропы, и явления локальные и случайные - с другой.

Все случаи, предполагаемые как реальные, разделим на два варианта: океан, насколько это возможно представить, или изолирован от обмена веществом и энергией с окружающей средой, или открыт для такого обмена. Можно утверждать, что преобладающая часть изолированного океана окажется однородной по составу и лишенной градиентов физических, химических и биологических характеристик. Это будет результатом диффузии - процесса, который неизбежен в любой жидкости и протекает в ней на много порядков быстрее, чем в твердых телах.

Из предыдущей главы ясно, почему изолированный океан будет однороден не полностью, а лишь в преобладающей части. Причина заключается в том, что даже при изоляции океана химически инертной оболочкой в нем останутся поверхностные или пограничные эффекты, связанные с избыточной свободной энергией поверхности раздела и проявляющиеся в увеличении физико-химической активности вещества.

Итак, независимо от размеров, формы и состава изолированного океана мы можем создать его словесную модель следующим образом: все внутреннее пространство океана представляет собой однородную, безградиентную, биологически малоактивную и химически сравнительно инертную область. Вся граничная поверхность покрыта тонкой активной пленкой. Между активной пленкой и инертной областью пролегает переходный слой, толщина которого будет тем больше, чем больше скорость диффузии.

Сила тяжести придает дополнительное значение верхней и нижней границам, сделав их местом накопления частиц, которые могут выделяться в результате, например, биологической деятельности и оказываться легче или тяжелее окружающей среды. При этом верхняя граница максимально обогатится легкими частицами и максимально обеднится тяжелыми, а донная граница будет обладать противоположным свойством. Процессы обеднения, вызванные силой тяжести, могут привести к тому, что оптимальные для развития жизни условия окажутся отодвинутыми по вертикали на какое-то расстояние от внешних границ океана. В том случае, когда океан разделен на слои разной плотности, возникают внутренние границы раздела, называемые скачками плотности. На глубине скачка плотности должно происходить обогащение воды как сравнительно тяжелыми частицами, опускающимися сверху, так и сравнительно легкими, всплывающими снизу.

Рассмотрим простейшую модель неизолированного океана. Неизолированность означает, что через граничные поверхности входят и выходят потоки энергии и вещества.

В идеально неизолированном океане с удалением от границ раздела потоки вещества и тепловой энергии не слабеют вследствие идеального (мгновенного) перемешивания, а потоки световой энергии не слабеют вследствие высокой прозрачности. Такой океан, как и идеально изолированный, окажется в преобладающей части однородным, однако все его внутреннее пространство будет во всех отношениях активной областью. Значения характеристик на некотором удалении χ от границы раздела будут сильно различаться в обоих океанах.

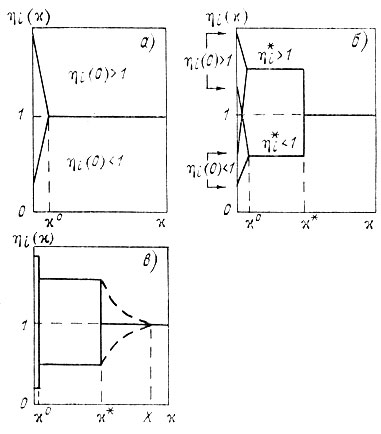
Рис. 10. Модели распределения свойств в идеальном океане с удалением от границы раздела. а - однослойный океан, б - двухслойный с идеально перемешиваемым пограничным слоем, в - схематическое изображение молекулярного подслоя в виде прямоугольного выстрела. Масштабы везде искажены.

Чтобы проводить сравнения, удобно пользоваться безразмерными характеристиками - отношением их значений в любой точке с_i (χ) к значениям на некотором достаточном удалении X от границы раздела c_i(X). Введем обозначение безразмерных характеристик ( Запись i = 1, т - удобное сокращение записи i = 1, 2, ..., т.):

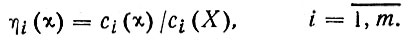
(16)

Общая картина распределения безразмерных характеристик η_i(χ) оказывается практически одинаковой в обоих идеализированных океанах (рис. 10 а), хотя и отличается в деталях.

Математически описать эту идеализованную картину, изображенную на рис. 10 а, можно следующим образом (Записи х ε [0, x⁰] и x ε[x⁰, ∞] означают множества решений неравенств 0 ≤x≤x⁰ и x⁰ ≤x<∞ соответственно.>):

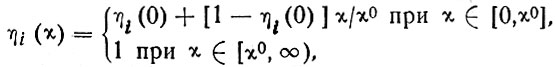
(17)

где х- расстояние от границы раздела, η_i(0)-значение η_i при х = 0, х^° - толщина пограничной пленки.

Следующим шагом будет комбинированная модель идеального океана. Часть океана, прилегающая к границе раздела, пусть будет идеально неизолированной, а сильно удаленная от границы - идеально изолированной. Тогда распределение безразмерных характеристик (16) должно показать две безградиентные области, резко различающиеся активностью и значениями η_i как показано на рис. 10 б. Здесь значения расстояния х и η_i в пределах идеально неизолированного слоя океана помечены звездочкой (х^* и η_i^*)-

Необходимо учесть, что в действительности с удалением от границ величина потоков вещества и энергии значительно меняется вследствие поглощения энергии и превращения (трасформации) веществ, причем не обязательно одинаково для всех. Рассмотрим положение, когда количество поглощаемой энергии и трансформированного вещества в единицу времени (их сток) можно считать пропорциональным концентрации упомянутых субстанций (в грубом приближении это справедливо для многих, процессов: поглощения лучистой энергии, потребления кислорода, потребления органического вещества и т. д.). Запишем, опустив для упрощения индекс i,

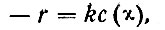
(18)

где r - количество расходуемой в единичном объеме и за единицу времени субстанции С (вещество или энергия), k - коэффициент пропорциональности, с (x)-количество (концентрация) субстанции С на расстоянии х от граничной поверхности.

Отметим, что величина расходуемой энергии и вещества (r) может служить количественной мерой активности процессов в соответствующем слое воды.

Рассмотрим широкую группу случаев, в которых движение можно считать однонаправленным. Подсчитаем баланс субстанции в слое толщиной dx. Поскольку мы хотим решить нестандартную по обобщению задачу, включающую разные ситуации - от потока лучистой энергии до потока падающих в воде частиц, будет уместно сделать пояснения. Пусть за единицу времени через поверхность единичной площади в слой войдет количество субстанции Wc, а выйдет из слоя через противоположную поверхность единичной площади количество субстанции W(c+dc), где W - скорость движения потока субстанции (будь то лучистая энергия, падающие или всплывающие с постоянной скоростью частицы и, наконец, субстанция, пассивно переносимая течением), a dc - уменьшение субстанций на пути dx. Общее количество субстанции, накапливающееся в слое dx (в расчете на единицу площади слоя и единицу времени), будет равно количеству входящей субстанции минус количество выходящей, т. е. - Wdc. Отнесем это накопление, разделив на dx, к кубику единичной толщины и обозначим q₀ где индекс «0» говорит о том, что накопление вызвано однонаправленным потоком

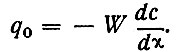
(19)

В стационарной задаче расход, определяемый уравнением (18), и накопление по уравнению (19) равны. Отсюда получаем следующее балансовое уравнение поля:

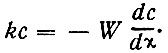
(20)

Когда одна и та же субстанция переносится одновременно несколькими способами, например, увлекается нисходящим течением со скоростью W₁ и одновременно обгоняет течение, падая в нем со скоростью W₂, балансовое уравнение будет иметь вид

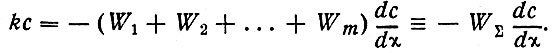
(21)

Интегрируя простое уравнение (20) или (21), разделив для этого переменные, получим экспоненциальный (логарифмический) закон уменьшения субстанции с удалением от границы раздела, например уменьшение светового потока с глубиной. Действительно, наши исходные рассуждения при выводе уравнений (19) и (20) справедливы и для уравнения светового поля (когда в нем для простоты пренебрегают диффузией света): количество лучистой энергии света, поглощаемое внутри слоя dx, равно разности светового потока, входящего через верхнюю границу слоя и выходящего через нижнюю. Поскольку скорость света (обозначим ее для общности W) постоянна, упомянутая разность будет определяться только изменением плотности светового потока на расстоянии dx и иметь выражение - Wdc. Для того чтобы математическая запись имела традиционный для светового потока вид, можно ввести коэффициент ослабления потока α, прямо пропорциональный поглощению потока и обратно пропорциональный его скорости:

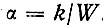
Теперь, используя в качестве граничного условия концентрацию с на поверхности с/_х=о = с(0), в результате интегрирования получим

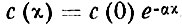
откуда

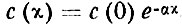
(22)

Подставляя выражение (22) в уравнение (18), получим

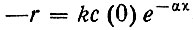
(23)

Из уравнения (22) видно, что активность процессов, измеряемая количеством энергии или вещества, расходуемым в единичном объеме воды за единицу времени, уменьшается с удалением от граничной поверхности по экспоненциальному закону.

Перейдем к случаю, когда распространение субстанции осуществляется в условиях встречных взаимопроникающих движений, как, например, при диффузии (будь то активная - молекулярная или лучистая - диффузия субстанции или пассивная диффузия, вызванная перемешиванием среды). Математическая модель диффузии вдоль оси строится из двух встречных однонаправленных потоков субстанции. Разность между ними составляет результирующий перенос через поверхность единичной площади (-Ddc/dx). Запишем, что перенос между точками 1 и 2 уменьшается вследствие того, что на пути dx часть потока со скоростью q_D переходит в накопление субстанции. Итак, уменьшение переноса равно накоплению субстанции:

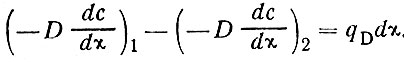
(24)

Отсюда при постоянном коэффициенте диффузии D накопление в единичном объеме и за единичное время равно

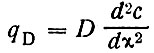
(25)

При стационарной задаче, когда накопление уничтожается потреблением, балансовое уравнение переноса, учитывая (18), запишется в следующем виде:

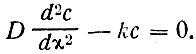
(26)

Теперь зададим граничные условия, и их должно быть два - соответственно второму порядку однородного дифференциального уравнения (26), так как при его интегрировании должны появиться две произвольные постоянные, которые необходимо будет определить с помощью граничных условий. Одно граничное условие - концентрация С на поверхности (с (0)) - использовалось выше. В качестве второго можно использовать условие однородности (безградиентности) на некотором (X) или бесконечно большом (х→∞) расстоянии от границы раздела.

Тогда уравнение (26) вместе с граничными условиями:

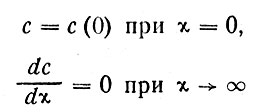
(27)

даст диффузионную модель распространения поглощающейся субстанции С.

Решение уравнения (26) складывается из экспонент, число которых равно порядку уравнения, т. е. в данном случае двум,

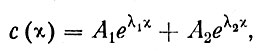
(28)

где λ₁, λ₂ - корни характеристического уравнения, соответствующего уравнению (26),

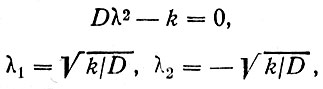
(29)

а A₁, A₂ - постоянные интегрирования.

Первое из граничных условий дает, с учетом уравнений (28) и (29), с(0) = А₁ + А₂. Согласно второму уравнению (27), величина с (x) не может безгранично возрастать или быть отрицательной, но это возможно лишь, если в уравнении (28) A₁ = 0. Следовательно, А₂ = с(0).

Таким образом, решение уравнения (26) дает снова экспоненциальное затухание величины концентрации и скорости потребления:

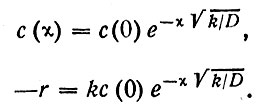
(30), (31)