Шаг к реальности. Эскиз модели открытого океана

В природных условиях чистых случаев одной диффузии или одной адвекции не бывает, имеет место какая-то комбинация этих процессов. С учетом этого в основу простейшей одномерной модели структуры открытого для обмена веществом и энергией океана следует положить балансовое уравнение одномерного поля, включающее диффузию в направлении оси 0х, различные однонаправленные потоки, а также источники, учитывающие расходование и образование субстанции, в частности ее убыль или прибыль в результате горизонтального переноса.

При стационарных условиях простейшее уравнение одномерного поля будет иметь вид

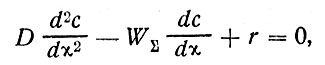
(32)

где r - мощность источника, задаваемая, например, уравнением (18).

Функция r может быть самой различной. Для простоты и определенности положим, что она состоит из двух слагаемых. Первое (w₀) выражает постоянную прибыль субстанции, второе - убыль субстанции, как и раньше, пропорциональную ее концентрации (в частном случае любое слагаемое может быть равным нулю),

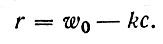
(33)

Примем вновь граничные условия (27). Решение неоднородного (с правой частью) дифференциального уравнения

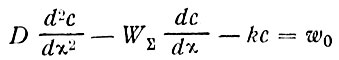
(34)

складывается из общего решения с_об.од соответствующего однородного уравнения (без правой части) и любого частного (с_ч.и) решения (частного интеграла) уравнения (34):

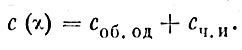
(35)

Общим решением с_об.од вновь будет выражение (28):

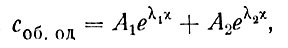
(36)

но значения корней λ₁ и λ₂ иные, так как характеристическое уравнение однородного уравнения, соответствующего (34) (без правой части), получающееся заменой d²c/dx² на λ², dc/dx на λ, а с на 1, будет следующим:

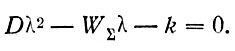
(37)

Корни этого уравнения

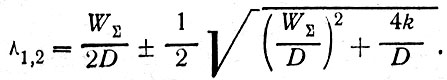
(38)

Частное решение с_{ч. и} уравнения (34) можно взять в виде некоторой постоянной А₃, значение которой легко получить, подставив значения с_{ч. И} = А₃ и ее производных в уравнение (34). Поскольку производные постоянной равны нулю, такая подстановка дает kc_{ч. и} = w₀ и

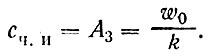
(39)

Как и в предыдущей задаче, поскольку величина с(х) не может безгранично возрастать, a λ₁>0, первое слагаемое в уравнении (36) должно быть равно нулю, что возможно лишь, если A₁=0. Учитывая это и подставляя (36) и (39) в решение (35), получим

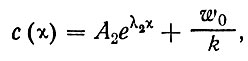
(40)

а используя первое из граничных условий (27)

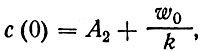
получим последнюю неизвестную постоянную

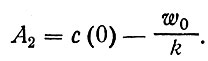
(41)

Подставляя значения постоянной А₂ (41) и λ₂ (38) в уравнение (40), получим окончательно

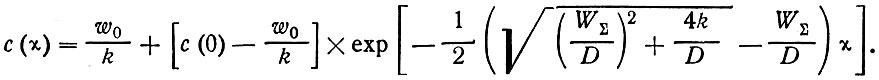
(42)

Согласно уравнению (42), существует предел

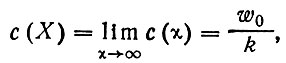
(42^')

который достигается «сверху» (понижением с(x) ) или «снизу» (повышением с(x) ), в зависимости от соотношения с(0) и w₀/k.

При с(0)>w₀/k уравнение (42) показывает экспоненциальное уменьшение количества переносимой субстанции по направлению к инертной области. При с(0)₀/k значение с(х) возрастает, пока не достигнет предельного значения с(Х). В решении могут появиться волны (промежуточные минимумы и максимумы) только в случае k<-W>²_Σ /4D. Отрицательные значения k соответствуют в уравнениях (33) и (34) автокатализу (самоускорению реакций) в химических системах; они обычны для биологических систем (имеют физический смысл удельной скорости размножения или продукции за вычетом смертности или метаболических потерь).

Решение (42) основано на предположении, что коэффициент диффузии D постоянен. В действительности это не так. Существует универсальный закон, по которому значения коэффициента растут от минимальных (молекулярных) D на границе раздела до максимальных К_x в области развитой турбулентности. Коэффициент молекулярной самодиффузии воды D имеет порядок 10^-5 см²/с; молекулярная диффузия господствует в тонкой поверхностной пленке толщиной порядка 10^-3 м. А, например, коэффициент развитой вертикальной турбулентной диффузии K_z имеет значение 10-10² см²/с и господствует в пограничном слое трения значительной толщины. Его значение в глубинных слоях океана оценивается в 1 см²/с. Мысленно подставляя в формулу (42) различные значения D и дифференцируя, легко представить, как изменяется наклон экспоненты к вертикальной оси 0Z глубин. При коэффициенте D наклон (на одинаковом расстоянии от граничной поверхности) будет примерно в 10⁵-10⁶ раз больше, чем при К_x. Аналогично изменится и картина горизонтального распределения от границы раздела (при горизонтальной шкале 0_х).

Не пытаясь найти здесь точное решение задачи с переменным коэффициентом диффузии D, мы можем, однако, сказать о тех качественных изменениях, которые испытает модель. В области околомолекулярных значений коэффициента D у границы раздела кривая претерпит излом и (при вертикальной шкале 0х), резко увеличив наклон, отойдет в сторону. Этим будет отмечена аномальная область поверхностной активной пленки. Изобразить такой малый структурный элемент на общей модели можно лишь символически, вне масштаба, например, прямоугольным выстрелом (см. рис. 10 в). В области максимальных значений коэффициента К_х кривая должна деформироваться противоположным образом - уменьшить наклон и принять направление, близкое к параллельному оси 0_x. Эта область (квазиоднородный слой интенсивного внутренного обмена и перемешивания) - активный пограничный слой, в пределах которого поглощается и трансформируется наибольшая часть энергии и вещества. Распределение субстанции в активном слое осложняют многие процессы, но учесть эти осложнения в обобщенной модели невозможно.

Постулируем, что непременной чертой всякого океана должны быть его значительные размеры, и определим эту значительность тем условием, что океан имеет большую протяженность, чем протяженность вторгающихся потоков вещества и энергии. Тогда мы должны будем выделить в океане инертную область, характеризующуюся исчезновением внешних потоков энергии и вещества, а также градиентов, замедлением процессов и реакций, бедностью проявлений жизни. Пограничный активный слой и удаленная от границ инертная область разделяются переходной зоной (пунктирная кривая на рис. 10 в), в которой экспоненциально затухает активность и могут прослеживаться остаточные явления сезонного хода характеристик.

Таков самый общий эскиз, максимально упрощенная, но типичная модель пространственной структуры океана. Типичная в том отношении, что она должна отражать наиболее существенные черты, наиболее общие и присущие всем океанам, и нивелировать региональные или временные особенности. Эта модель пока что одномерна и стационарна, поскольку она описывает закономерные изменения в одном направлении - перпендикулярном какой-либо граничной поверхности - и основана на предположении сбалансированности скоростей поступления и исчезновения субстанции в каждой точке пространства (dc/dt=0), что может быть верным лишь среднестатистически и не всегда.

Если попытаться снять эти упрощения, то получить аналитические решения соответствующих уравнений становится трудно, и обычно удается реализовать модели лишь с помощью ЭВМ. Если же и удается получить аналитические решения, они все равно слишком сложны и громоздки для практического использования.

Полученная модель открытого океана оказывается похожей по характеру распределения в нем субстанции на идеальный «комбинированный» океан, рассмотренный выше.

Обращает на себя внимание то, казалось бы, парадоксальное обстоятельство, что модель открытого океана включает элементы, из которых строилась и модель изолированного океана, и при этом не противоречит нашим представлениям о реальном океане. Причина здесь в том, что проницаемость воды для вторгающихся в океан потоков - света, количества движения, тепла, растворимых веществ - ограничена. Учитывая замутненность природных вод, наклон проникающих в воду лучей и альбедо поверхности, можно предполагать, что в среднем всего 1 - 2% водной толщи океана получают лучистую энергию в количестве не менее 1% суммарной радиации, падающей на поверхность воды. Глубина, до которой посредством трения распространяется поток количества движения, зависит от географической широты места, устойчивости ветра и плотностной стратификации воды. Можно ориентировочно полагать, что в среднем по площади и по времени эта глубина близка к 1 - 2% средней глубины океана. Средняя для океана глубина проникновения сезонного хода температуры и концентрации растворенных веществ имеет порядок 10² м. Тот же порядок имеет глубина распространения фитопланктона. Учитывая приведенные оценки, а также взаимодействие океана с берегом и дном, можно полагать, что слой (оболочка) океана, открытый для непосредственного обмена через граничные поверхности, составляет около 2% объема всех океанических вод. Это сопоставимо с полным объемом вод суши. На инертную область океана, область, бедную жизнью, малоградиентную, с вяло протекающими процессами и временем оборота органического вещества порядка 10³ лет, приходится около 75% объема, а остальное - на переходную зону.

Для более подробного сравнения модели с действительными распределениями удобно опять использовать безразмерную характеристику η(x) = с(х)/с(Х).

Таким образом, эскиз упрощенной одномерной модели пространственной структуры океана должен включать описание следующих подразделений, начиная от каждой границы в океане:

1) поверхностной пленки η = η^° при х∈[0, х^°),

2) активного пограничного слоя η = η^* при х∈(х^°, х^*)

3) переходной зоны

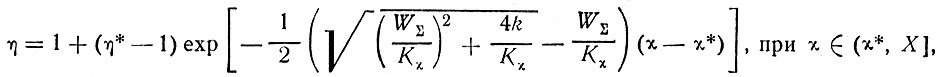
(43)

4) инертной области η = l при

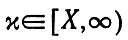
или в более компактной записи:

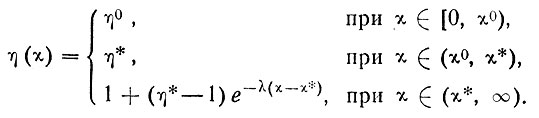
(44)

Последнее из трех выражений в записи (44) описывает одновременно переходную и инертную области.

Следовательно, по вертикали, от свободной поверхности до дна, можно выделить всего 𕟹 структурных подразделений.

В случае конкретных пограничных слоев и субстанций по-разному получаются выражения для η^°, η^* и потоков обмена субстанцией на границах между структурными подразделениями I, 2, 3. Последние нужны для склейки единой математической модели. Однако здесь, при максимально генерализованном и упрощенном описании достаточно ограничиться эскизной моделью (44) с непрерывными функциями, претерпевающими излом на внутренних границах раздела слоев x⁰ и x^*. Графики, соответствующие модели (44), представлены кривыми 1 на рис. 11. Кривые 2 и 3 - различные варианты упомянутых уточнений, учета возможности k>0 в случае биологических систем и т. д. - приведены, чтобы показать, сколь несущественны для интересующего нас здесь общего вопроса такие уточнения, хотя они и весьма важны в частных задачах.

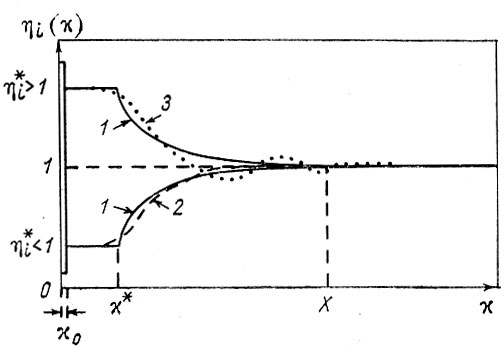
Рис. 11. Модель с переходным слоем.

Определение параметра λ эскизной модели (44) легко провести по данным типового распределения субстанции с помощью полулогарифмической анаморфозы, получающейся из выражений (44),

(45)

Значение параметра λ, как видно из уравнения (45), равно тангенсу угла наклона прямой в координатах

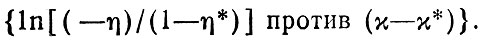
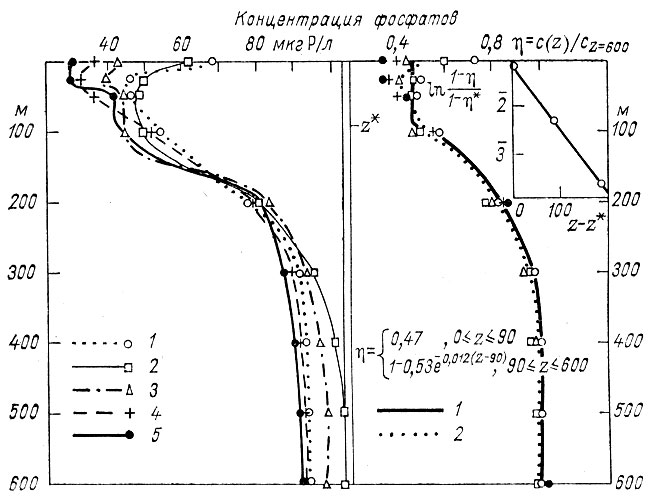
Рис. 12. Вертикальное распределение фосфатов на одной из станций в Тихом океане. Слева: 1 - январь, 2 - март, 3 - май, 4 - июль, 5 - август («Химия Тихого океана», 1966); справа; 1 - модельный профиль (44), 2 - кривая, усредненная по всем данным наблюдений; на врезке показан способ расчета параметров модели.

На рис. 12 приведено вертикальное распределение фосфатов на одной из станций PAPA в Тихом океане в различные сезоны, полученное В. В. Сапожниковым и В. В, Мокиевской [Химия Тихого океана, 1966], а кроме того, эти же данные представлены в виде относительных (безразмерных) единиц концентраций. Сравнение показывает: как ни абстрактна модель (44), она способна дать общее представление о характере распределения субстанции. Однако чтобы отразить обычно наблюдающийся промежуточный максимум фосфатов, необходимы уточнения и детализации, а также учет внутренних границ раздела в толще вод (жидких и границы вода-живое вещество).

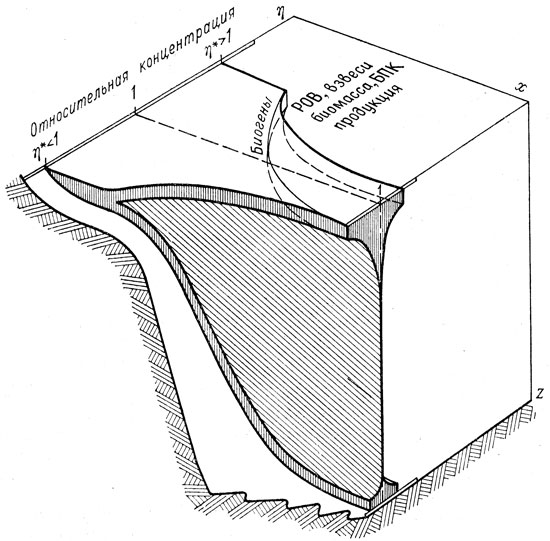
Рис. 13. Генерализованная модель циркумграничной структуры океана.

На рис. 13. показана комбинация модельных горизонтальных и вертикальных профилей с учетом трех границ-свободной (с атмосферой), с берегом и с дном.