Почему возникают пленки? Ответ второй

Предположим, что профиль ветра в пограничном слое образован трением, которое во много раз превосходит отклоняющую силу вращения Земли, и потому последней можно пренебречь. Мысленно разрежем воздушный поток на множество тонких пластинок, выберем любую из них и подумаем, при каких условиях ее скорость будет постоянной. Сверху на пластинку действует сила трения τ₁, которая стремится ускорить пластинку, передавая ей движение от верхней, более быстрой. Снизу действует сила трения τ₂, которая тормозит пластинку о нижнюю, более медленную. Следовательно, условием того, чтобы скорость пластинки не менялась под действием трения, является равенство τ₁ = τ₂. Продолжая эти рассуждения для других слоев, получим, что устойчивость профиля ветра сохранится в случае, если трение останется постоянным в любой по высоте точке, пока можно пренебрегать силой Кориолиса, возрастающей с ростом скорости движения слоя.

Предположим далее, что кинетическая энергия хаотических турбулентных пульсаций скорости внутри каждого слоя постоянна во времени. Это постоянство всегда достигается при динамическом равновесии, т. е. в результате того, что приход турбулентной энергии равен ее расходу. Кинетическая энергия равна половине произведения массы на квадрат скорости. Кинетическую энергию турбулентности, отнесенную к единице массы, определяют так:

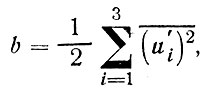
(54)

где и₁, и₂, и₃ - пульсации скорости по осям х, у, z.

Считают, что скорость изменения турбулентной энергии в единице неподвижного объема пространства складывается из двух главных процессов

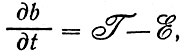
(55)

где

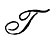
- генерация турбулентной энергии,

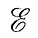
- превращение механической энергии в тепло.

Заметим в скобках, что более детальные модели учитывают превращения энергии за счет плавучести (положительной и отрицательной) и диффузии энергии вместе с носителем.

Генерация турбулентной энергии происходит из энергии трения, связанной со сдвигом (вихрем) средней скорости, например с ее изменением по высоте. Каскад превращений энергии на удалении от граничной поверхности выразим записью

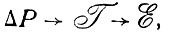
(56)

где ΔР- энергия сдвига средней скорости (вихревая энергия).

У поверхности

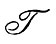
=0, поэтому звено

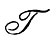
схеме (56) выпадает и энергия сдвига должна переходить в тепло, минуя пульсации. Проследим за этим. Когда скорость ветра уменьшается сверху вниз, в том же направлении передается поток кинетической энергии. Какова же скорость поступления энергии в единичный объем горизонтального слоя воздуха? Согласно определению понятий работа, энергия, мощность, эта скорость равна произведению силы на путь точки приложения силы, деленный на время, т. е.

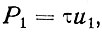
(57)

где и₁ - скорость движения воздуха на верхней границе слоя.

Однако не вся поступающая энергия может обратиться в турбулентную. Часть ее, рассекая слой, выйдет через его нижнюю границу. Эта часть

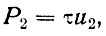
(58)

где и₂-скорость движения воздуха на нижней границе слоя.

Энергия, получаемая единицей объема воздуха, равна разности величин входящего и выходящего потоков энергии, отнесенной к толщине слоя. При постоянном τ

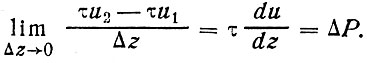
(59)

Если в объеме не возникают ускорение и пульсации, вся поглощаемая энергия ΔР должна отводиться в тепло посредством молекулярной вязкости

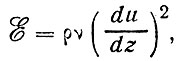
(60)

где v - коэффициент кинематической вязкости, р - плотность воздуха.

Поскольку в пределах молекулярного подслоя скорость ветра изменяется линейно, запишем

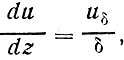
(61)

где и_δ-скорость ветра на верхней границе молекулярного подслоя, δ - толщина подслоя.

Понятно, что определять и_δ очень трудно, поэтому желательно иметь в модели неизменную по высоте характеристику скорости ветра. Такую характеристику (скорость трения) получают из условия, что приземный ветер установился. Мы помним, что в этом случае трение τ становится постоянным по высоте. На граничной поверхности τ₀, как известно из опытов, пропорционально квадрату скорости:

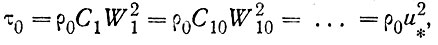
(62)

где С - коэффициент трения, W - скорость ветра в м/с, индексы 0, 1, 10 - высота в м, и_*-скорость трения в м/с.

Величины С, и_* находят по эпюре скорости. Они связаны формулой

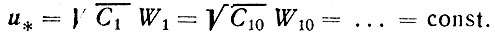
(63)

Опыты вблизи Цингста дали С₁₀= 1,3х10^-7. У дна моря этот коэффициент, вероятно, на 4-5 порядков больше.

Запишем условия существования молекулярного подслоя так: вся получаемая этим слоем энергия сдвига средней скорости переходит непосредственно в тепло

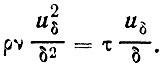
(64)

Подставив выражение- (62) в (64), найдем толщину молекулярного подслоя

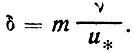
(65)

где т = и_δ/и*.

По наблюдениям вблизи Цингста т = 7,7 при δ в мм, v в см²/с, и_* в см/с

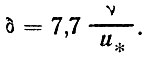
(66)

Известно, что при аэродинамически гладком обтекании твердой стенки на ее поверхности возникает вязкий молекулярный подслой высотой

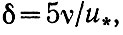
за которым до высоты 70 v/и_* расположена переходная ламинарно-турбулентная область потока [Шлихтинг, 1956].

Сложные модели, включающие иерархию пограничных слоев и их взаимодействие с движущимися волнами, рассматриваются в монографии «Процессы переноса вблизи поверхности раздела океан - атмосфера» [1974] и в других работах, которые, несмотря на их исключительно интересное содержание, мы не имеем возможности здесь затронуть.