
Загадочный однородный слой океана, он же - главный пограничный слой
Вслед за первым пограничным слоем океана - молекулярной пленкой - выделяют второй, или главный, пограничный слой, толщина которого имеет порядок 102 м, а состояние характеризуется турбулентностью.
Понятие "пограничный слой" было введено в механику сплошных сред в 1904 г. Л. Прандтлем, оно означает "пограничная зона", в которой нельзя правильно описать движение жидкости, пренебрегая ее внутренним трением. В связи с этим пограничный слой называют также вязким слоем, или слоем трения. Название «вязкий» справедливо и для молекулярного слоя-пленки.
Первый парадокс главного пограничного слоя состоит в сочетании огромных различий (размеры) и глубокого сходства (вязкости) с первым слоем - пленкой. Внутреннее трение (или вязкость) жидкости, согласно гипотезе Ньютона, есть сила, пропорциональная градиенту скорости. Коэффициент пропорциональности носит название коэффициента вязкости. Для ламинарного движения гипотеза строго подтверждается опытом и имеет силу закона
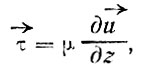
(69)
где
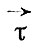
- вектор силы трения, отнесенный к единичной
площадке,
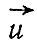
- вектор скорости, μ - коэффициент молекулярной вязкости, имеющий для воды при 20°С значение 10-3 и для воздуха 2х10-5 кг/(мхс).
Турбулентная форма движения была исследована О. Рейнольдсом лишь в 1883 г., и еще в начале нашего века геофизики пытались применить уравнение (69) с молекулярными коэффициентами вязкости к океанским течениям. В дальнейшем выяснилось, что гипотеза Ньютона очень грубо учитывает трение и в турбулентном потоке, но лишь в случае, когда молекулярную вязкость как бы превращают в турбулентную умножением на число, величина которого может достигать 10 000. Одновременно с этим в формулу подставляется осреднениое значение скорости. Чтобы вязкость т сохранялась в прежних пределах, градиент скорости должен быть, как видно из формулы (69), уменьшен соответственно в 10 000 раз.
Это означает, что прежняя величина вязкости достигается с помощью нового условия - относительной однородности осредненной скорости, малым ее изменением с глубиной.
Вслед за понятием «динамический пограничный слой» возникли понятия «температурный» и «диффузионный пограничный слой», отражающие воздействие границы на поле температуры и поля растворенных или взвешенных веществ.
Вторую особенность главного пограничного слоя составляет его резкая нижняя граница. Согласно теории Прандтля, пограничный слой постепенно, асимптотически переходит в область, не затронутую влиянием границы (внепограничную). Однако турбулентный слой океана реагирует на многие воздействия как единое целое, сохраняя квазиоднородную по вертикали структуру и резкую нижнюю границу.
Основным аппаратом исследования пограничного слоя становится теория подобия, которая позволяет упрощать уравнения процесса путем усложнений их членов [Китайгородский, 1970]. Задача вычисления толщины квазиоднородного пограничного слоя пока что отсутствует в учебниках океанологии, если не считать наиболее простого случая - плотно-стной конвекции при охлаждении или осолонении поверхности. Попытаемся все-таки взглянуть на подход к решению, используя простые условия и традиционную форму записи.
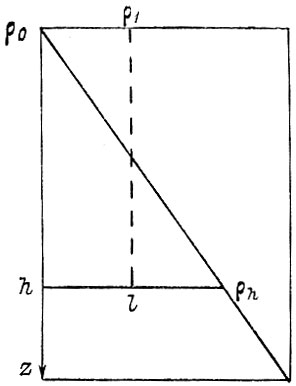
Рис. 26. Увеличение потенциальной энергии воды в процессе перемешивания (потенциальная энергия массы hρsub0/subρsubh/sub соответствует началу перемешивания, она меньше потенциальной энергии массы hρsub0/subρsub1/subl).
Возьмем за основу рассуждений тот факт, что при формировании однородного слоя воды путем ветрового перемешивания (а не конвекции!) потенциальная энергия водной массы повышается. Это не вполне очевидное утверждение поясним рис. 26 и расчетом.
Пусть в начальный момент времени однородного слоя не было, и плотность воды равномерно повышалась с глубиной по линии ρ0 (на поверхности) - ρh (на глубине h). Потенциальная энергия Е1 в этом случае будет связана с фигурой ρ0hρh на рис. 26.
После того как слой 0-h будет перемешан, его потенциальная энергия Е2, отнесенная к единице площади поверхности, увеличится и будет соответствовать фигуре ρ0ρ1lh. Приращение потенциальной энергии в результате перемешивания получается в виде разности ЕП=Е2 - Е1
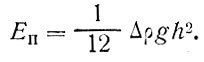
(70)
Таким образом, мы узнали, какую цену в единицах энергии надо заплатить за создание перемешанного слоя. Осталось определить поступление энергии.
Допустим, что оно равно притоку кинетической энергии в воду от воздействия ветра. Скорость поступления энергии за счет силы трения, как уже говорилось, равна силе, умноженной на путь точки приложения силы (работа) и деленной на время (мощность). Это будет полное поступление кинетической энергии τи которая затем распределяется и трансформируется во всей толще воды (или воздуха), расположенной ниже уровня действия τ. На рис. 27 прямоугольниками показано поглощение энергии в слоях движущейся воды при различных эпюрах скорости. Расстояния между вертикальными линиями пропорциональны силе трения, а длина слоя, включая прямоугольник, равна величине скорости в этом слое.
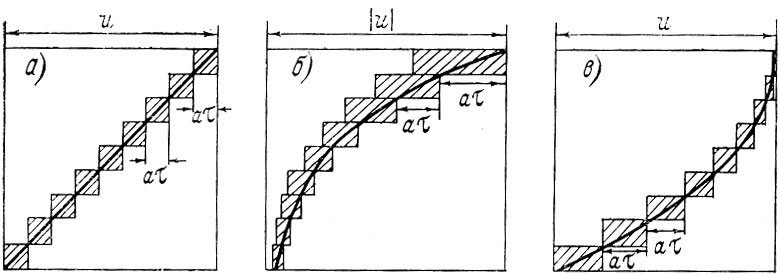
Рис. 27. Величина энергии, диссипируемой в турбулентность и теплоту в равновесных эпюрах. Поглощение энергии показано прямоугольниками. а - линейная, вызванная постоянным трением; б - экмановская, вызванная трением и уравновешенная силой Кориолиса; в - вызванная градиентом давления и уравновешенная трением.
Принципиальный интерес представляет линейная эпюра, стоящая первой. Хотя источник потерь энергии - исчезновение скорости в нижней точке, общая сумма потерь равномерно распределена по всей толще воды и равна работе трения ветра о верхнюю границу потока. Куда же уходит энергия? Очевидно, рассеивается (диссипирует) в турбулентные пульсации. Однако если турбулентность стационарна, то этот переход - промежуточная инстанция, через которую поток энергии должен проходить без потерь и затем трансформироваться частично в тепло, а частично в потенциальную энергию. Последний процесс, как мы видели, осуществляется путем изменения плотностной стратификации воды.
Самым грубым и простым способом выразим поток входящей энергии:
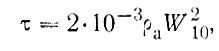
(71)
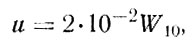
(72)
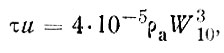
(73)
где τ - сила трения в нхм2, ρа - плотность воздуха в кг/м3, W10 -скорость ветра на высоте 10 м в м/с, и - скорость поверхностного течения в м/с.
Теперь можно составить баланс. Формула толщины перемешанного ветром слоя получится при приравнивании уравнения (70) к уравнению (73), умноженному на время действия ветра t,
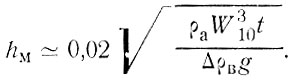
(74)
Единицы измерения плотности атмосферы ρа и воды ρв в выражении (74) могут быть любыми, кроме единицы условной плотности (σt), остальные величины выражены в системе СИ. Чтобы узнать приращение толщины перемешанного слоя Δh, формулу (74) придется использовать дважды: определить h1, h2 и найти разность.
Предложенное выше решение демонстрирует тенденцию не использовать коэффициент турбулентной диффузии К. Модели процесса с этим коэффициентом называются К-моделями, они имеют свои слабые стороны, как отмечает Е. Б. Краус [1976]. Однако эти модели вносят дополнительную ясность в физическую картину процесса. В рамках К-моделей принимается зависимость коэффициента турбулентной диффузии от устойчивости, которая пропорциональна градиенту плотности. При развитии градиента плотности происходит запирание верхнего слоя.
|
ПОИСК:
|
© UNDERWATER.SU, 2001-2019
При использовании материалов проекта активная ссылка обязательна:
http://underwater.su/ 'Человек и подводный мир'
При использовании материалов проекта активная ссылка обязательна:
http://underwater.su/ 'Человек и подводный мир'