Может ли главный пограничный слой океана служить поглотителем атмосферных загрязнений?

Хотя развитие физической теории главного пограничного слоя океана стимулировалось необходимостью решать задачи гидротермодинамики океана, по-видимому, наиболее важной областью ее применения окажется обслуживание экологических задач. Одна из таких задач- проблема загрязнения атмосферы галогенугле-водородами, особенно хлорфторметанами CCl₃F и CCl₂F₂, при фотолизе которых образуются очень активные атомы галогенов. Такое загрязнение чревато разрушением озонного экрана биосферы, поглощающего губительные ультрафиолетовые лучи. Способен ли океан поглощать и очищать атмосферу от этих загрязнений?

Рассмотрим простую модель поглощения главным пограничным слоем океана хлорфторметанов (ХФМ), предложенную К. Юнге [Junge, 1976].

Пусть скорость глобального поступления (выбрасывания) ХФМ в воздух составляет p(t), и они равномерно распределяются в атмосфере, а перенос в стратосферу пренебрежимо мал. Тогда концентрацию ХФМ в приводном слое атмосферы (с_a) Юнге определяет выражением

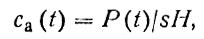
(75)

где

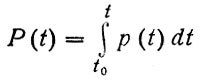
(76)

есть общее количество ХФМ, поступивших в атмосферу за время от начального до t, s - площадь поверхности Земли, Н - толщина атмосферы.

Диффузионный ток ХФМ из атмосферы в океан (q₁) через пограничный подслой описывается, как это делалось выше,

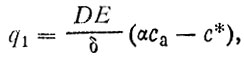
(77)

где, как и раньше, α - растворимость ХФМ в воде, с^* - концентрация ХФМ на нижней границе пограничного подслоя.

Главный пограничный слой считаем однородным, и, следовательно, концентрация ХФМ в нем равна с^*, а количество ХФМ в столбе воды пограничного слоя на единицу площади равно hc^* (если объем воды в выражении концентрации дается в тех же единицах, что и толщина слоя h, например в кубических метрах и метрах соответственно).

Количество ХФМ в столбе воды пограничного слоя уменьшается при переносе их вниз (поток q₂) и при реакциях (сток q₃).

Юнге допускает, что концентрация ХФМ в переходном слое пренебрежимо мала по сравнению с с^* и записывает поток q₂ с помощью очень простого и традиционного для таких задач выражения

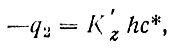
(78)

где K^,_z - скорость обмена пограничного слоя с переходным.

Распад (сток q₃) ХФМ Юнге описывает общепринятым способом: как реакцию первого порядка с константой распада k. Т. е. для столба воды главного пограничного слоя сток

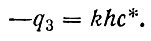
(79)

Из этих простых соображений получается балансовое соотношение: изменение количества ХФМ в столбе воды пограничного слоя есть алгебраическая сумма всех трех потоков

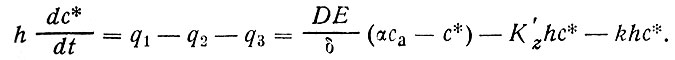
(80)

Отсюда получается уравнение изменения концентрации ХФМ в главном пограничном слое

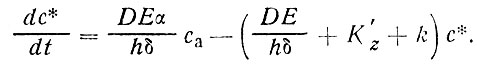
(81)

Таким образом, для расчета концентрации или количества ХФМ в пограничном слое океана кроме режима загрязнения атмосферы надо уметь рассчитывать толщину пограничного слоя, определять толщину молекулярно-диффузионного (ламинарного) подслоя δ, интегральный коэффициент Е, а также скорость обмена K^'_z и константу распада k. Каждая из этих задач имеет свои трудности. Сравнительно легко измеряется лишь растворимость α и коэффициент диффузии D.

Юнге взял значения, которые считал типичными для океана (среднюю толщину ламинарного подслоя δ = 0,07 мм, главного пограничного слоя h = 50 м, К^'_z = 2x10^-9с^-1) и для галогеноуглеводородов (D=lx10^-5 см²/с, Е=1, растворимость α от 0,12 до 0,046, константу распада k - порядка 10^-7 с^-1, т. е. порядка 0,01 сутки^-1). Распределение их количества можду атмосферой и океаном, учитывая, конечно, площадь Мирового океана, он рассчитал на ЭВМ но уравнениям (75) и (81), задавшись близким к действительности экспоненциально растущим загрязнением атмосферы ХФМ. Проигрывая на ЭВМ различные варианты - меняя значения параметров в интервалах, которые могут наблюдаться, - он пришел к общему выводу: даже при благоприятных условиях в пограничном слое поглощение ХФМ океаном не превышает нескольких процентов годового поступления их в атмосферу, и, следовательно, океан не может служить поглотителем ХФМ из атмосферы. Поскольку в модели Юнге не использовал предположения и схемы химического характера, выводы и ее саму он распространяет и на другие газообразные загрязнители атмосферы, особенно органические, имеющие тот же порядок величины растворимости а и константы распада k.

Вот мы и получили малоутешительный, но, видимо, в общем правильный ответ на вопрос, поставленный в названии этого параграфа. Однако снова просматривая ход построения профессором Юнге этой модели от уравнения (75) до уравнения (81), читатель, возможно, обратит внимание на то, что фигурирующая в обоих этих уравнениях величина концентрации загрязнителя в атмосфере с_а (t) задана лишь скоростью производства загрязнителя (75). Между тем и для атмосферы следует решать задачу о концентрации в ней загрязнителя, как для главного пограничного слоя. То есть надо тоже учесть диффузионный поток q₁ (77) через «ламинарный» пограничный подслой из атмосферы в океан. Но для этого надо знать с^*, а чтобы ее рассчитать, надо в свою очередь знать с_а. Следовательно, обе задачи следует решать совместно.

Предположим, что приходная часть (источник) в уравнении скорости изменения количества загрязнителя в столбе пограничного слоя атмосферы толщиной h_a известна:

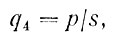
(82)

а в расходную часть (сток), кроме диффузионного потока в океан (77) и потока вышележащие слои атмосферы, где с_а будем считать пренебрежимо малой,

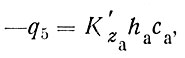
входит также распад загрязнителя в пограничном слое атмосферы, который опишем самым простым из возможных способом, т. е. также уравнением реакции первого порядка

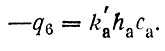
(83)

Обозначив

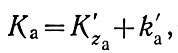
опишем изменение количества загрязнителя для столба пограничного слоя атмосферы

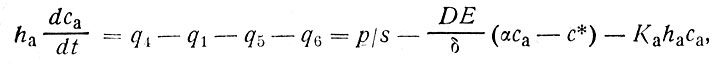
(84)

а для системы источник загрязнения - атмосфера - океан получим систему из трех уравнений:

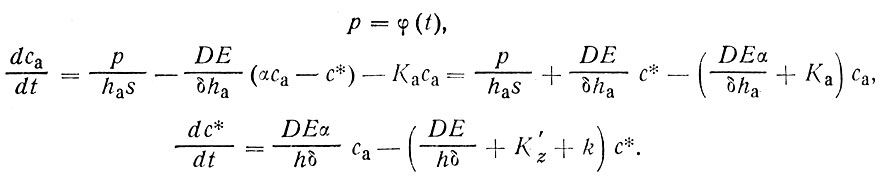
(85)

Ее легко решить численно с помощью ЭВМ, но можно решить и аналитически, если считать, что в атмосфере из-за ее большей подвижности поле концентраций устанавливается быстрее, чем в пограничном слое океана. При условии квазистационарности dc_a/dt = 0 второе уравнение системы (85) становится алгебраическим; решая его, получим выражение для концентрации загрязнителя в атмосфере

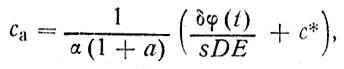
(86)

где

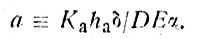
(87)

Подставляя выражение (86) в последнее уравнение системы (85), получим после преобразований

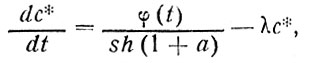
(88)

где обозначено

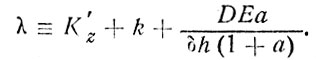
(89)

Теперь зададим начальное условие и закон функционирования источника загрязнения, т. е. вид функции φ(t). Пусть в момент, от которого мы начинаем отсчет времени (t = 0), имеется определенная концентрация загрязнителя в главном пограничном слое, т. е. начальное условие

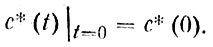
(90)

Рассмотрим два источника загрязнения: стационарный и экспоненциально возрастающий.

Стационарный источник φ(t) =p(0) = const.

В этом случае получаем линейное однородное уравнение, в котором легко разделяются переменные

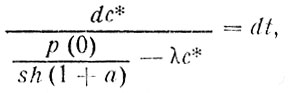
а интеграл от левой части - табличный. Переписав его из любого справочника и использовав начальное условие (90), получим искомое решение

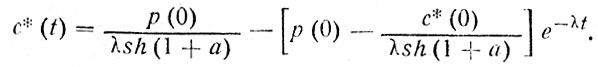
(91)

Подставляя это выражение для с^* (t) в уравнение (86), получим уравнение изменения концентрации загрязнителя в атмосфере

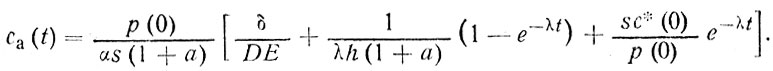
(92)

С помощью уравнений (91) и (92) легко рассчитать, как изменяется со временем концентрация загрязнителя в атмосфере и в океане, надо лишь задать численные значения величин, входящих в уравнения (91) и (92).

Из уравнений (91) и (92) видно, что, поскольку λ>0 при достаточно большом времени

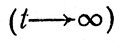
экспонента становится равной нулю и в системе устанавливаются стационарные концентрации

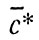
и

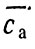
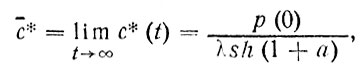
(93)

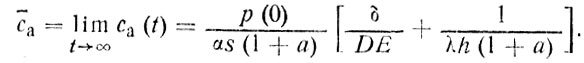
(94)

Время достижения стационарных концентраций (t) можно оценить по отношению

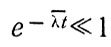
Так, при λ порядка 10^-7 с^-1 оно составляет около полугода. Приходится помнить, что эти рассуждения действительны лишь до тех пор, пока концентрацию загрязнителя в глубинах океана можно считать пренебрежимо малой.

Из выражений (93) и (94) можно также оценить соотношение количества загрязнителя в атмосферном (М_a) и в океаническом (М^*) пограничных слоях

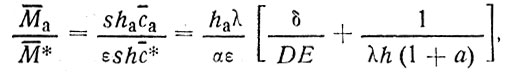
(95)

где ε = 0,71 - доля поверхности Мирового океана в общей поверхности Земли. Подставляя использовавшиеся Юнге величины в соотношение (95), получим M_а/M^* порядка 10², т. е. подавляющая часть загрязнения находится в атмосфере. Однако концентрация загрязнителя в атмосфере, как это легко аналогичным образом под-считывается, выше, чем в пограничном слое океана, всего лишь на порядок.

Экспоненциальный источник

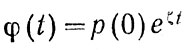
(96)

Он больше соответствует сегодняшнему положению дел. Получить аналитическое решение уравнения (88), а затем и выражение (86) при экспоненциальном источнике тоже очень просто.

Подставим функцию (96) в уравнение (88) и получим неоднородное (с первой частью) дифференциальное уравнение

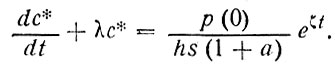
(97)

Следуя простому классическому способу решения таких уравнений, сначала ищем общее решение (с^*_{об. од} ) соответствующего (97) однородного уравнения (без правой части):

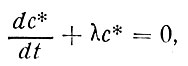
что - очень легко сделать, разделив переменные

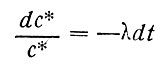
и взяв табличный интеграл, а затем пропотенцировав полученное выражение,

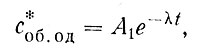
(98)

где А₁ - постоянная интегрирования.

Далее надо использовать любое частное решение (частный интеграл) (с^*_{ч. и}) уравнения (97). Рекомендуется брать его в виде

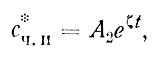
(99)

где А₂ - постоянная, которую надо найти.

Подставляя это с^*_{ч. и} и ее производную

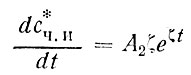
в уравнение (97)

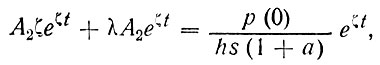
получим значение постоянной А₂

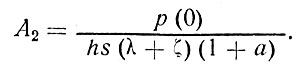
(100)

Теперь, суммируя

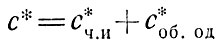
и используя начальное условие (90), получим соотношение

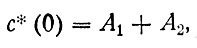
из которого находим значение постоянной

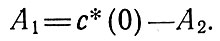
Общим решением уравнения (97)

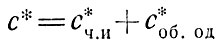
таким образом, будет

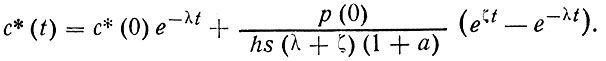
(101)

А подставляя выражение для c^*(t) (101) в уравнение (86), получим уравнение изменения концентрации загрязнителя в атмосфере

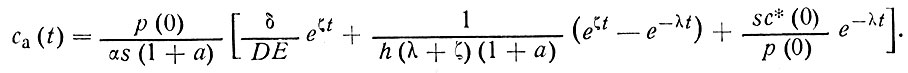
(102)

Из уравнений (101) и (102) видно, что по прошествии сколь угодно большого времени, хотя члены, содержащие ехр (-λt), обращаются в нуль, концентрация загрязнителя как в атмосфере, так и в океане продолжает экспоненциально возрастать по законам:

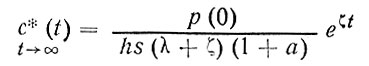
(103)

и

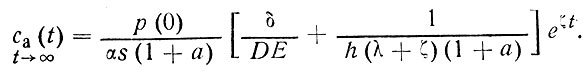
(104)

Однако при этом соотношение концентрации (и количества) загрязнителя в атмосфере и океане остается постоянным:

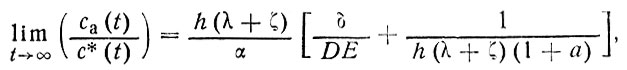
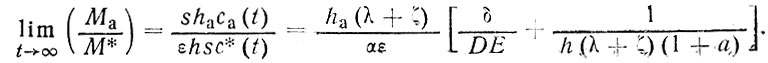
(105)

При

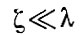
(если использовать численные значения, принятые Юнге, то λ имеет порядок

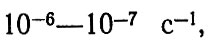
а

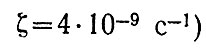
как видно из сравнения соотношений (105) и (95), распределение загрязнителя между атмосферой и океаном не зависит от режима источника загрязнения - при достаточно большом времени t, порядка 10⁶ - 10⁷ с (несколько месяцев).

Остается рассмотреть, по какому закону при этом будут изменяться доли накапливающегося в атмосфере и в океане количества загрязнений от общей массы загрязнений, выброшенной в атмосферу P(t).

Учитывая, что

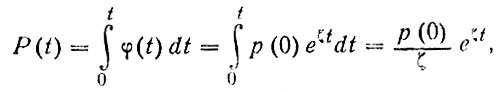
получим, используя выражения (103) и (104), что при

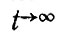
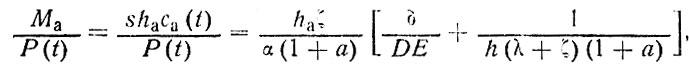
(106)

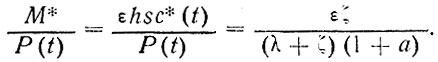
(107)

Искомые доли, как ни странно, остаются постоянными, несмотря на накапливание загрязнений, т. е. это накапливание прямо пропорционально суммарной массе выброшенных загрязнителей.

Можно было бы, используя имеющиеся ориентировочные численные значения параметров, охарактеризовать цифрами распределение и потоки загрязнителей. Однако оценки для большинства параметров пока слишком грубы, а для многих отсутствуют. Так, нет сколько-нибудь надежных оценок констант распада загрязнителей в природных условиях. Но не всегда для правильных выводов и нужны знания этих констант.

Например, относительно галогенуглеводородов вывод, сделанный Юнге, подтверждается, если для них действительно коэффициент растворимости а составляет около 0,1, Е = 1, а k>1x10^-7 с^-1 (k≥0,01 сутки^-1). И этот вывод поразителен. Какие бы большие константы распада k мы ни подставляли в выражение для λ (89) и в уравнение (106), мы не обнаружим никакого эффекта, в том числе улучшения самоочищения от загрязнения в системе атмосфера - океан: второе слагаемое в управлении (106) все время остается пренебрежимо малым по сравнению с первым, характеризующим пограничный молекулярно-диффузионный подслой, δ/DE. Это означает следующее типичное для океана и биосферы вообще обстоятельство, осознать которое удается лишь с трудом: судьба загрязнителей в многокилометровых толщах атмосферы и океана всецело определяется ситуацией, складывающейся в пограничном молекулярно-диффузионном (ламинарном) подслое океана ничтожной толщины, 0,01 - 0,1 мм. Из-за плохой пропускной способности этой пленки по отношению к слабо растворимым ХФМ океан не способен очищать атмосферу от них и им подобных загрязнителей, даже если и мог бы быстро их перерабатывать в безопасные продукты. В этом заключается как их опасность, так и возможность при необходимости регулировать процессы в многокилометровой толще биосферы путем не требующих сравнительно больших усилий воздействий на процессы в микроструктурах, например в данном случае, влияя на значение интегрального коэффициента Е пленки или подбирая вещества с необходимыми значениями α.

Конечно, стремясь получить здесь наиболее простые и доступные решения, мы, как и профессор Юнге, допускали некоторые вольности, которые скажутся на результатах, если попытаться получить точные численные характеристики. Однако были важны не сами цифры - 90 или 60% загрязнителей скапливается в атмосфере - хотя это весьма существенно. Здесь мы преследовали иную цель: показать канву, по которой можно двигаться, стремясь построить простые генерализованные модели трансформации веществ при взаимодействии океана и атмосферы на основе элементов теории главного пограничного слоя океана.